Your Chebyshevs inequality example images are available. Chebyshevs inequality example are a topic that is being searched for and liked by netizens now. You can Download the Chebyshevs inequality example files here. Download all royalty-free photos.
If you’re searching for chebyshevs inequality example images information related to the chebyshevs inequality example topic, you have visit the right blog. Our site frequently gives you suggestions for seeing the maximum quality video and picture content, please kindly search and find more informative video content and images that match your interests.
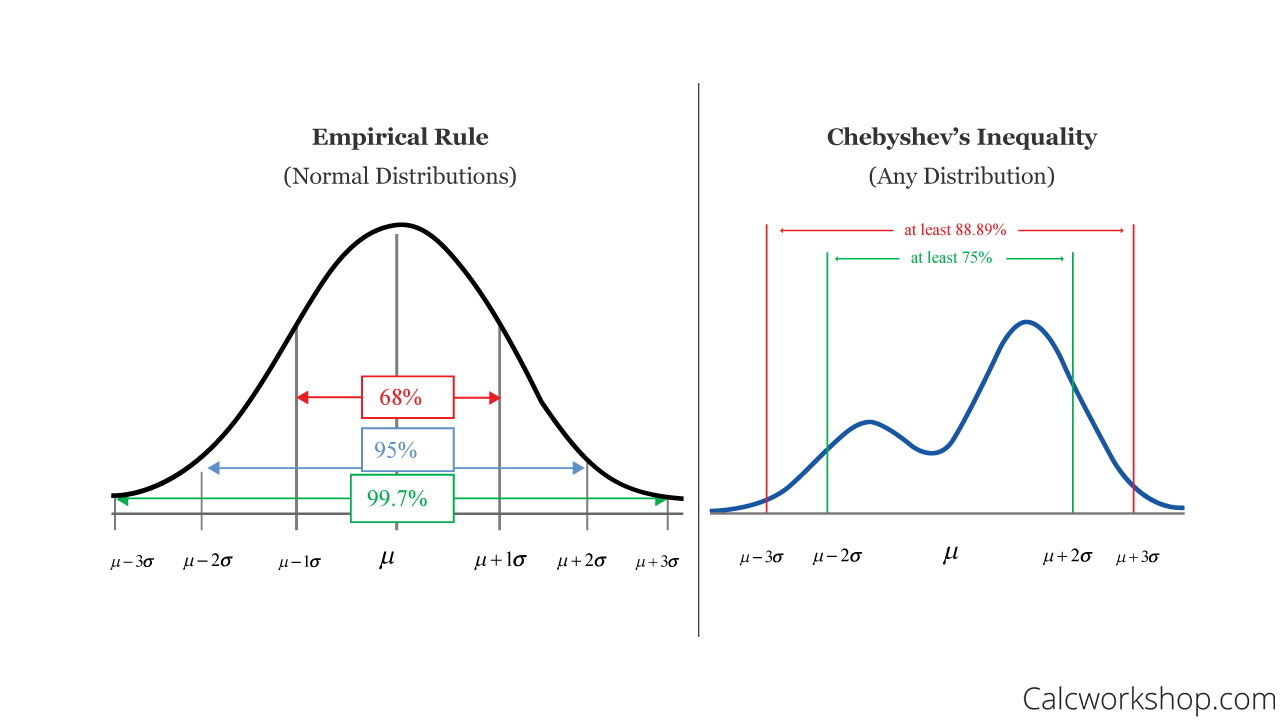
Chebyshevs Inequality Example. The Pareto distribution is the PDF fx cxp for x 1 and 0 otherwise. Example of Chebyshevs inequality. In probability theory Chebyshevs inequality guarantees that for a wide class of probability distributions no more than a certain fraction of values can be more than a certain distance from the mean. So Chebyshevs inequality says that at least 9375 of the data values of any distribution must be within two standard deviations of the mean.
The Chebyshev Inequality Part Ii Inference Limit Theorems Introduction To Probability Mit Opencourseware From ocw.mit.edu
Also find the bound when p 1 2 and alpha 3 4. We demonstrate with examples. Lets use Chebyshevs integral inequality to solve Problem 2. The Pareto distribution is the PDF fx cxp for x 1 and 0 otherwise. Chebyshevs Inequality Formula P 1 1 k2 P 1 1 k 2 Where P is the percentage of observations. Chebyshevs inequality says that at least 1-1K2 of data from a sample must fall within K standard deviations from the mean here K is any positive real number greater than one.
Example Suppose we have sampled the weights of dogs in the local animal shelter and found that our sample has a mean of 20 pounds with a standard deviation of 3 pounds.
There are two forms. In this video we are going to prove Chebyshevs Inequality whi. Example Problem Statement Use Chebyshevs theorem to find what percent of the values will fall between 123 and 179 for a data set with mean of 151 and standard deviation of 14. The standard deviation of the distribution in question is. Practical Example Assume that an asset is picked from a population of assets at random. However Chebyshevs inequality is true for all data distributions not just a normal distribution.
Source: slidetodoc.com
In this video we are going to prove Chebyshevs Inequality whi. However Chebyshevs inequality is true for all data distributions not just a normal distribution. So Chebyshevs inequality says that at least 9375 of the data values of any distribution must be within two standard deviations of the mean. PjX j. Chebyshevs inequality says that at least 1-1K2 of data from a sample must fall within K standard deviations from the mean here K is any positive real number greater than one.
Source: youtube.com
Chebyshevs inequality Examples of Markovs and Chebyshevs inequalities Weak Law of Large Numbers Central Limit theorem Example of the Central Limit theorem Central Limit theorem for independent random variables Strong Law of Large Numbers One Sided Chebyshev Inequality Examples Chernoff Bound. Let us say that Random Variable R IQ of a random person. Use Chebyshevs inequality to approximate the proportion of bottles that contain at least 33 ounces or at most 31 ounces of fruit juice. Chebyshevs inequality gives a bound on the probability that X is far from its expected value. Example 1 Suppose that is a random variable with mean 16 and variance 16.
Source: youtube.com
Taking the bounded set as the ball centered at the origin with radius δ 0 for example for the above Burgers Equation 468 with multiplicative noise we have. Suppose a fair coin is ipped 100 times. Using Chebyshevs Inequality calculate the upper bound on P X αn where alpha lies between pa and 1. This video provides a proof of Chebyshevs inequality which makes use of Markovs inequality. The rule is often called Chebyshevs theorem about the range.
Source: youtube.com
Taking the bounded set as the ball centered at the origin with radius δ 0 for example for the above Burgers Equation 468 with multiplicative noise we have. The quality control engineer at the bottling plant desires the amount of soft drink to be. Chebyshevs Inequality Formula P 1 1 k2 P 1 1 k 2 Where P is the percentage of observations. Chebyshevs Inequality Concept 1Chebyshevs inequality allows us to get an idea of probabilities of values lying near the mean even if we dont have a normal distribution. Example of Chebyshevs inequality.
Source: studylib.net
Consider a random variable X that follows Binomial distribution with parameters n p. Example Suppose we have sampled the weights of dogs in the local animal shelter and found that our sample has a mean of 20 pounds with a standard deviation of 3 pounds. Chebyshevs inequality theorem is one of many eg Markovs inequality theorem helping to describe the characteristics of probability distributions. Let us say that Random Variable R IQ of a random person. Below you can find some exercises with explained solutions.
Source: slidetodoc.com
Chebyshevs inequality – Example 1 - YouTube. Let be a random variable such that. The rule is often called Chebyshevs theorem about the range. For example two-thirds of the observations fall within one standard deviation on either side of the mean in a normal distribution. PjX j.
Source: chegg.com
Chebyshevs inequality has many applications but the most important one is probably the proof of a fundamental result in statistics the so-called Chebyshevs Weak Law of Large Numbers. There are two forms. Example Problem Statement Use Chebyshevs theorem to find what percent of the values will fall between 123 and 179 for a data set with mean of 151 and standard deviation of 14. And average IQ of a person is 100 ie Ex R 100. Let us say that Random Variable R IQ of a random person.
Source: youtube.com
Example Problem Statement Use Chebyshevs theorem to find what percent of the values will fall between 123 and 179 for a data set with mean of 151 and standard deviation of 14. Practical Example Assume that an asset is picked from a population of assets at random. The amount of soft drink in ounces to be filled in bottles has a mean of ounces and has a standard deviation of ounces. Let us say that Random Variable R IQ of a random person. Let and See that is decreasing on the interval So since is increasing we have by Chebyshevs.
Source: ocw.mit.edu
But if the data set is not distributed in the shape of a bell curve then a different amount could be within one standard deviation. If we set a k where is the standard deviation then the inequality takes the form PjX j k VarX k 2 1 k2. The Pareto distribution is the PDF fx cxp for x 1 and 0 otherwise. Put to get Since both functions and are decreasing on the interval we have by Chebyshevs inequality and Remark 1 Example 2. Specifically no more than 1k2 of the distributions values can be k or more standard deviations away from the mean.
Source: calcworkshop.com
However Chebyshevs inequality is true for all data distributions not just a normal distribution. Chebyshevs inequality theorem is one of many eg Markovs inequality theorem helping to describe the characteristics of probability distributions. Lets understand the concept with the help of an example for better understanding as follows. Use Chebyshevs inequality to approximate the proportion of bottles that contain at least 33 ounces or at most 31 ounces of fruit juice. The Pareto distribution is the PDF fx cxp for x 1 and 0 otherwise.
Source: youtube.com
However Chebyshevs inequality is true for all data distributions not just a normal distribution. Using the Chebyshev inequality we can estimate the likelihood of solution orbits remaining inside or outside of a bounded set in Hilbert space H L20l. Also find the bound when p 1 2 and alpha 3 4. Chebyshevs inequality – Example 1 - YouTube. Example 1 Suppose that is a random variable with mean 16 and variance 16.
Source: stats.stackexchange.com
Solution We subtract 151-123 and get 28 which tells us that 123 is 28 units below the mean. The following gives a lower bound for the first probability. The rule is often called Chebyshevs theorem about the range. Example of Chebyshevs inequality. Example Suppose we have sampled the weights of dogs in the local animal shelter and found that our sample has a mean of 20 pounds with a standard deviation of 3 pounds.
Source: medium.com
In this video we are going to prove Chebyshevs Inequality whi. Taking the bounded set as the ball centered at the origin with radius δ 0 for example for the above Burgers Equation 468 with multiplicative noise we have. However Chebyshevs inequality goes slightly against the 68-95-997 rule commonly applied to the normal distribution. Chebyshevs inequality theorem is one of many eg Markovs inequality theorem helping to describe the characteristics of probability distributions. The quality control engineer at the bottling plant desires the amount of soft drink to be.
Source: chegg.com
Chebyshevs inequality says that at least 1-1K2 of data from a sample must fall within K standard deviations from the mean here K is any positive real number greater than one. However Chebyshevs inequality is true for all data distributions not just a normal distribution. Practical Example Assume that an asset is picked from a population of assets at random. And Variance in R is 15. PjX j.
Source: math.stackexchange.com
This video provides a proof of Chebyshevs inequality which makes use of Markovs inequality. Chebyshevs inequality has many applications but the most important one is probably the proof of a fundamental result in statistics the so-called Chebyshevs Weak Law of Large Numbers. But if the data set is not distributed in the shape of a bell curve then a different amount could be within one standard deviation. The rule is often called Chebyshevs theorem about the range. A Numerical Example Suppose a fair.
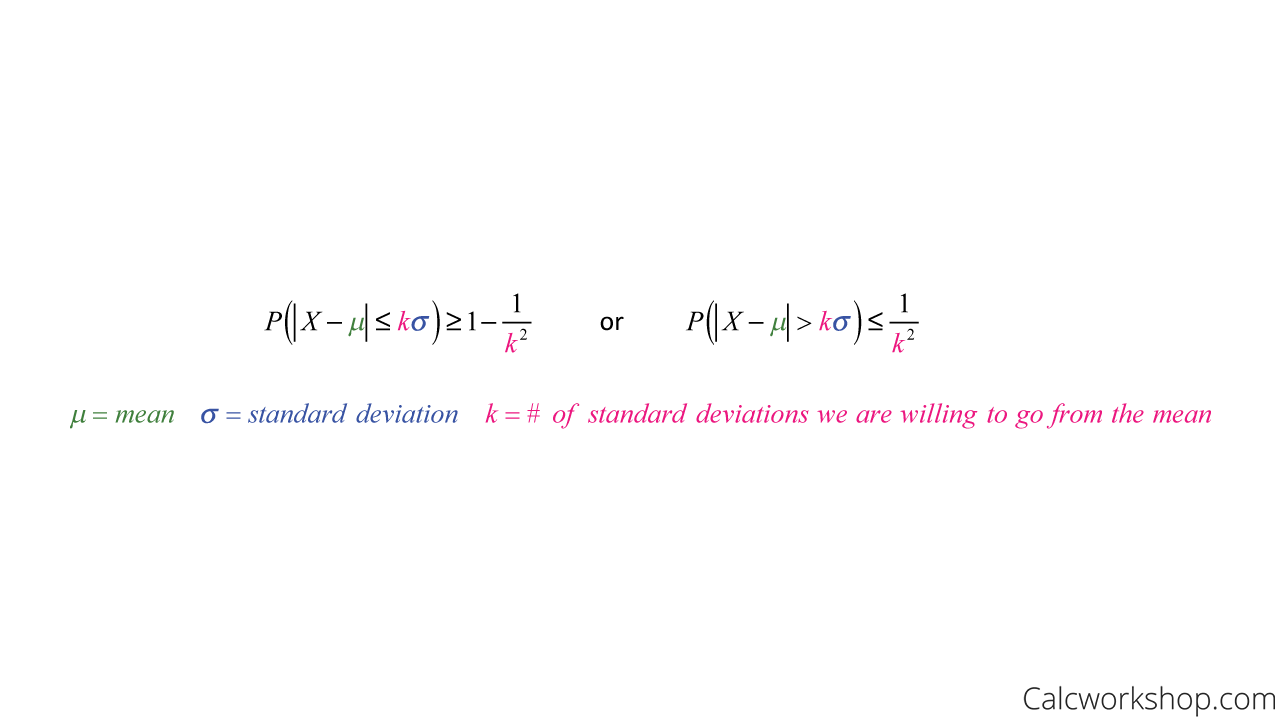Source: calcworkshop.com
The standard deviation of the distribution in question is. But if the data set is not distributed in the shape of a bell curve then a different amount could be within one standard deviation. In probability theory Chebyshevs inequality guarantees that for a wide class of probability distributions no more than a certain fraction of values can be more than a certain distance from the mean. PjX j. Chebyshevs Inequality Statement Let X be a random variable with a finite mean denoted as µ and a finite non-zero variance which is denoted as σ2 for any real number K0.
Source: slideplayer.com
The Pareto distribution is the PDF fx cxp for x 1 and 0 otherwise. So Chebyshevs inequality says that at least 9375 of the data values of any distribution must be within two standard deviations of the mean. Use Chebyshevs inequality to find a lower bound for the following. We demonstrate with examples. A Financial Example Lets compare the Dow Jones and NASDAQ stock market returns over the last 40.
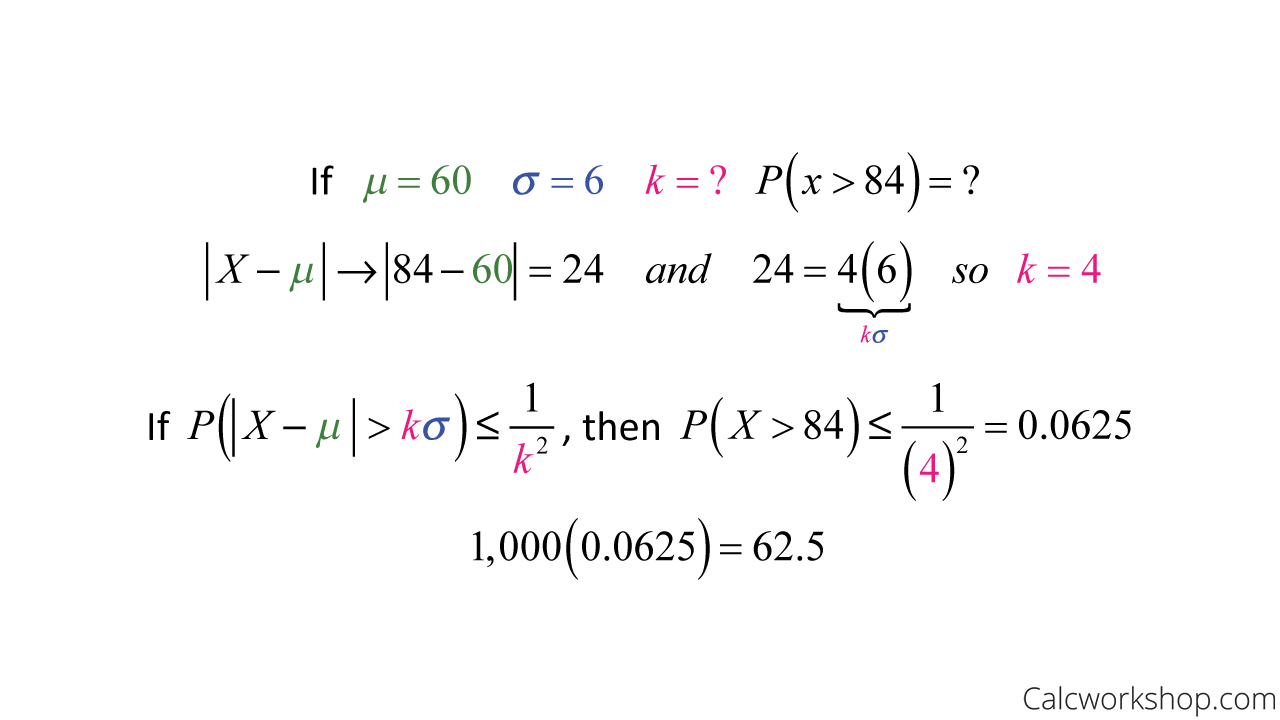Source: calcworkshop.com
In probability theory Chebyshevs inequality guarantees that for a wide class of probability distributions no more than a certain fraction of values can be more than a certain distance from the mean. However Chebyshevs inequality is true for all data distributions not just a normal distribution. Use Chebyshevs inequality to find a lower bound for the following. Lets understand the concept with the help of an example for better understanding as follows. Chebyshevs Inequality - Example Example Suppose we randomly select a journal article from a source with an average of 1000 words per article with a standard deviation of 200 words.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title chebyshevs inequality example by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
