Your Gram schmidt process example images are ready in this website. Gram schmidt process example are a topic that is being searched for and liked by netizens now. You can Get the Gram schmidt process example files here. Get all free vectors.
If you’re searching for gram schmidt process example images information connected with to the gram schmidt process example interest, you have pay a visit to the right blog. Our site always gives you suggestions for refferencing the maximum quality video and picture content, please kindly surf and locate more enlightening video content and graphics that match your interests.
Gram Schmidt Process Example. V1v2 is an orthogonal basis for Span x1x2. Ad Build your Career in Data Science Web Development Marketing More. Therefore given a non-orthonormal basis it is desirable to have a process for obtaining an orthonormal basis from it. 79 Gram-Schmidt Process P.
Gram Schmidt Procedure Mathematics Stack Exchange From math.stackexchange.com
Let w1 x1 kx1k v2 x2 hx2w1iw1 v3 x3 hx3w1iw1. Invest 2-3 Hours A Week Advance Your Career. 1 Gram-Schmidt process Consider the GramSchmidt procedure with the vectors to be considered in the process as columns of the matrix A. Suppose A a1 a2. Let v1 x1 and v2 x2 x2 v1 v1 v1 v1. The Gram-Schmidt process is an important algorithm that allows us to convert an arbitrary basis to an orthogonal one spanning the same subspace.
79 Gram-Schmidt Process P.
Therefore given a non-orthonormal basis it is desirable to have a process for obtaining an orthonormal basis from it. 79 Gram-Schmidt Process P. Ad Build your Career in Data Science Web Development Marketing More. Suppose is a linearly independent subset of Then the Gram-Schmidt orthogonalisation process uses the vectors to construct new vectors such that for and for This process proceeds with the following idea. Its just an orthogonal basis whose elements are only one unit. Let be a finite dimensional inner product space.
Source: coursehero.com
Eigenvalues and eigenvectors of a matrix. Gram-Schmidt Process proju uv vu uu Where uv denotes the inner product of the vectors u and v. Gram-Schmidt Orthogonalization We have seen that it can be very convenient to have an orthonormal basis for a given vector space in order to compute expansions of arbitrary vectors within that space. When we studied elimination we wrote the process in terms of matrices and found A LU. If youre not too sure what orthonormal means dont worry.
Source: youtube.com
Flexible Online Learning at Your Own Pace. Let v3 x3 x3 v1 v1 v1 v1 x3 v2 v2 v2 v2 component of x3 orthogonal to Span x1x2 Note that v3 is in WWhy. U2 a2 a2 e1e1. V1v2 is an orthogonal basis for Span x1x2. Using Gram-Schmidt to find an orthonormal basis for a plane in R3Watch the next lesson.
Source: math.stackexchange.com
1 Gram-Schmidt process Consider the GramSchmidt procedure with the vectors to be considered in the process as columns of the matrix A. Given an arbitrary basis u 1 u 2 u n for an n -dimensional inner product space V the. V1v2 is an orthogonal basis for Span x1x2. We learn about the four fundamental subspaces of a matrix the Gram-Schmidt process orthogonal projection and the matrix formulation of the least-squares problem of drawing a straight line to fit noisy data. The Gram-Schmidt process is an important algorithm that allows us to convert an arbitrary basis to an orthogonal one spanning the same subspace.
Source: youtube.com
If youre not too sure what orthonormal means dont worry. Suppose x1x2xn is a basis for an inner product space V. V1v2v3 is an orthogonal basis for W. Welcome to the Gram-Schmidt calculator where youll have the opportunity to learn all about the Gram-Schmidt orthogonalizationThis simple algorithm is a way to read out the orthonormal basis of the space spanned by a bunch of random vectors. A similar equation A QR relates our starting matrix A to the result Q of the Gram-Schmidt process.
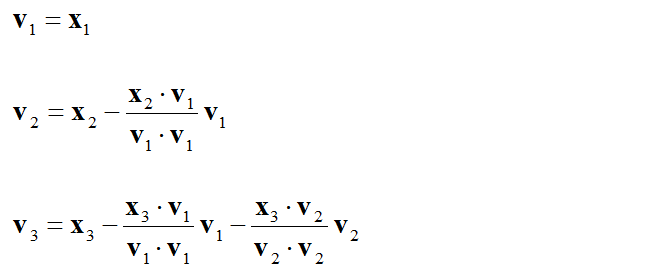Source: sharetechnote.com
Let be a finite dimensional inner product space. Orthogonality and the Gram-Schmidt Process In Chapter 4 we spent a great deal of time studying the problem of finding a basis for a vector space. Where L was lower triangular R is upper triangular. Let V be a subspace of mathbbRn of dimension k. We know that a basis for a vector space can potentially be chosen in many different ways.
Source: khanacademy.org
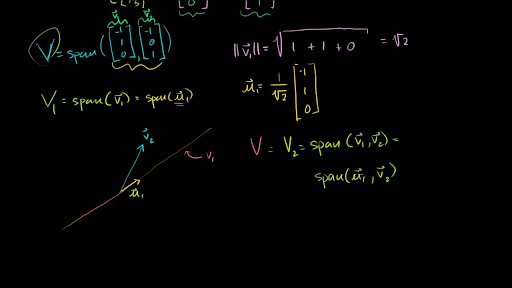
Suppose A a1 a2. Welcome to the Gram-Schmidt calculator where youll have the opportunity to learn all about the Gram-Schmidt orthogonalizationThis simple algorithm is a way to read out the orthonormal basis of the space spanned by a bunch of random vectors. Step 1 Let v 1 u 1. Gram-Schmidt Orthogonalization We have seen that it can be very convenient to have an orthonormal basis for a given vector space in order to compute expansions of arbitrary vectors within that space. Let V be a subspace of mathbbRn of dimension k.
Source: math.stackexchange.com
1 Gram-Schmidt process Consider the GramSchmidt procedure with the vectors to be considered in the process as columns of the matrix A. Flexible Online Learning at Your Own Pace. Its just an orthogonal basis whose elements are only one unit. Danziger 1 Orthonormal Vectors and Bases De nition 1 A set of vectors fv i j1 i ngis orthogonal if v iv j 0 whenever i6 jand orthonormal if v iv j ˆ 1 i j 0 i6j For ease of notation we de ne the the Kronecker delta function. 0 1 and B2 3 1.
Source: chegg.com
E1 u1 jju1jj. A Q R T a 1 q1 a 2 Tq a 1. Uk1 ak1 ak1 e1e1. Where L was lower triangular R is upper triangular. We look at how one can obtain an orthonormal basis for V starting with any basis for V.
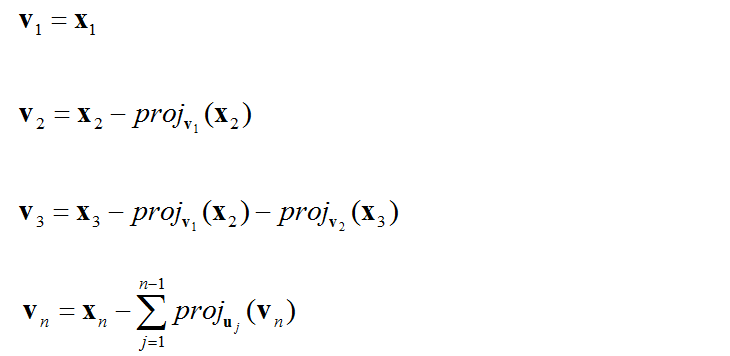Source: sharetechnote.com
We learn some of the vocabulary and phrases of linear algebra such as linear independence span basis and dimension. The Gram-Schmidt process is an important algorithm that allows us to convert an arbitrary basis to an orthogonal one spanning the same subspace. Let v1 x1 and v2 x2 x2 v1 v1 v1 v1. Gram-Schmidt Process proju uv vu uu Where uv denotes the inner product of the vectors u and v. Where L was lower triangular R is upper triangular.
Source: slideshare.net
Let v3 x3 x3 v1 v1 v1 v1 x3 v2 v2 v2 v2 component of x3 orthogonal to Span x1x2 Note that v3 is in WWhy. Example of Gram-Schmidt orthogonalization. Then u1 a1. Let V be a subspace of mathbbRn of dimension k. Suppose A a1 a2.
Source: youtube.com
Given an arbitrary basis u 1 u 2 u n for an n -dimensional inner product space V the. 2 2 both form bases for R2. V1v2v3 is an orthogonal basis for W. 116 0 but are not orthogonal. We will now apply Gram-Schmidt to get three vectors w 1 w 2 w 3 which span the same subspace in this case all R 3 and orthogonal to each other.
Source: khanacademy.org
That is A a1 fl fl a 2 fl fl fl fl a n. A Q R T a 1 q1 a 2 Tq a 1. Constructs an orthogonal basis v 1 v 2 v n for V. We learn some of the vocabulary and phrases of linear algebra such as linear independence span basis and dimension. We will now apply Gram-Schmidt to get three vectors w 1 w 2 w 3 which span the same subspace in this case all R 3 and orthogonal to each other.
Source: sciencedirect.com
Ad Build your Career in Data Science Web Development Marketing More. THEOREM 11 THE GRAM-SCHMIDT PROCESS. Let v1 x1 and v2 x2 x2 v1 v1 v1 v1. We learn about the four fundamental subspaces of a matrix the Gram-Schmidt process orthogonal projection and the matrix formulation of the least-squares problem of drawing a straight line to fit noisy data. Example of Gram-Schmidt orthogonalization.
Source: khanacademy.org
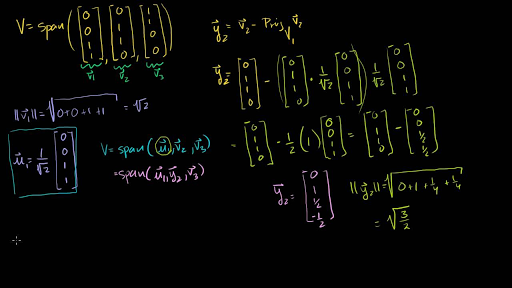
Invest 2-3 Hours A Week Advance Your Career. 1 Gram-Schmidt process Consider the GramSchmidt procedure with the vectors to be considered in the process as columns of the matrix A. In this post we will implement and visualize this algorithm in 3D with a popular Open. 116 0 but are not orthogonal. We learn about the four fundamental subspaces of a matrix the Gram-Schmidt process orthogonal projection and the matrix formulation of the least-squares problem of drawing a straight line to fit noisy data.
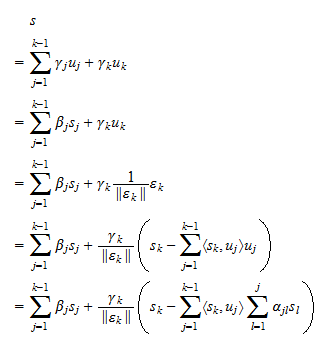Source: statlect.com
Let v1 x1 and v2 x2 x2 v1 v1 v1 v1. Therefore given a non-orthonormal basis it is desirable to have a process for obtaining an orthonormal basis from it. We look at how one can obtain an orthonormal basis for V starting with any basis for V. Let v3 x3 x3 v1 v1 v1 v1 x3 v2 v2 v2 v2 component of x3 orthogonal to Span x1x2 Note that v3 is in WWhy. Step 2 Let v 2 u 2 u 2 v 1 v 1 2 v 1.
Source: nptel.ac.in
Welcome to the Gram-Schmidt calculator where youll have the opportunity to learn all about the Gram-Schmidt orthogonalizationThis simple algorithm is a way to read out the orthonormal basis of the space spanned by a bunch of random vectors. Suppose is a linearly independent subset of Then the Gram-Schmidt orthogonalisation process uses the vectors to construct new vectors such that for and for This process proceeds with the following idea. Method is the Gram-Schmidt process. We learn about the four fundamental subspaces of a matrix the Gram-Schmidt process orthogonal projection and the matrix formulation of the least-squares problem of drawing a straight line to fit noisy data. A worked example of the Gram-Schmidt process for finding orthonormal vectorsJoin me on Coursera.
Source: study.com
A similar equation A QR relates our starting matrix A to the result Q of the Gram-Schmidt process. E1 u1 jju1jj. Let V be a subspace of mathbbRn of dimension k. Orthogonality and the Gram-Schmidt Process In Chapter 4 we spent a great deal of time studying the problem of finding a basis for a vector space. We will now apply Gram-Schmidt to get three vectors w 1 w 2 w 3 which span the same subspace in this case all R 3 and orthogonal to each other.
Source: math.stackexchange.com
We will now apply Gram-Schmidt to get three vectors w 1 w 2 w 3 which span the same subspace in this case all R 3 and orthogonal to each other. Invest 2-3 Hours A Week Advance Your Career. First we take w 1 v 1 3 0 4. 116 0 but are not orthogonal. 1 a2 q1 q2 a 1 Tq 2 a 2 Tq 2.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title gram schmidt process example by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
