Your Greens theorem example images are ready. Greens theorem example are a topic that is being searched for and liked by netizens now. You can Find and Download the Greens theorem example files here. Get all royalty-free images.
If you’re searching for greens theorem example images information linked to the greens theorem example interest, you have visit the right site. Our site frequently gives you hints for seeking the maximum quality video and image content, please kindly hunt and locate more enlightening video articles and images that match your interests.
Greens Theorem Example. 1 per month helps. Greens theorem articles Greens theorem. Lets see if we can use our knowledge of Greens theorem to solve some actual line integrals. Circulation Form of Greens Theorem.
Introduce Green S Theorem Explained Visually For Beginners Theorems Data Visualization Software Math Methods From pinterest.com
But with simpler forms. A planimeter is a device used for measuring the area of a region. Ab R2 is a piecewise. Circulation Form of Greens Theorem. We are taking C to have positive orientation. All of the examples that I.
We are taking C to have positive orientation.
This entire section deals with multivariable calculus in the plane where we have two integral theorems the fundamental theorem of line integrals and Greens theorem. Where C is the CCW-oriented boundary of upper-half unit disk D. Greens Theorem Cauchys Theorem Cauchys Formula These notes supplement the discussion of real line integrals and Greens Theorem presented in 16 of our text and they discuss applications to Cauchys Theorem and Cauchys Formula 23. It allows us to find the relationship between the line integral and double integral this is why Greens theorem is one of the four core concepts of the fundamental theorem of Calculus. Since D D is a disk it seems like the best way to do this integral is to use polar coordinates. We could compute the line integral directly see below.
Source: pinterest.com
But with simpler forms. Greens theorem articles Video transcript. To indicate that an integral C is. It allows us to find the relationship between the line integral and double integral this is why Greens theorem is one of the four core concepts of the fundamental theorem of Calculus. The first form of Greens theorem that we examine is the circulation form.
Source: pinterest.com
Greens Theorem - Example 1 In mathematics Greens theorem also known as the divergence theorem or the fundamental theorem of calculus is a theorem in calculus in which the integral of a function over an arbitrary region in the plane is found by computing the line integral around any closed curve that intersects the region. We are taking C to have positive orientation. It allows us to find the relationship between the line integral and double integral this is why Greens theorem is one of the four core concepts of the fundamental theorem of Calculus. Circulation Form of Greens Theorem. The tangent vector.
Source: pinterest.com
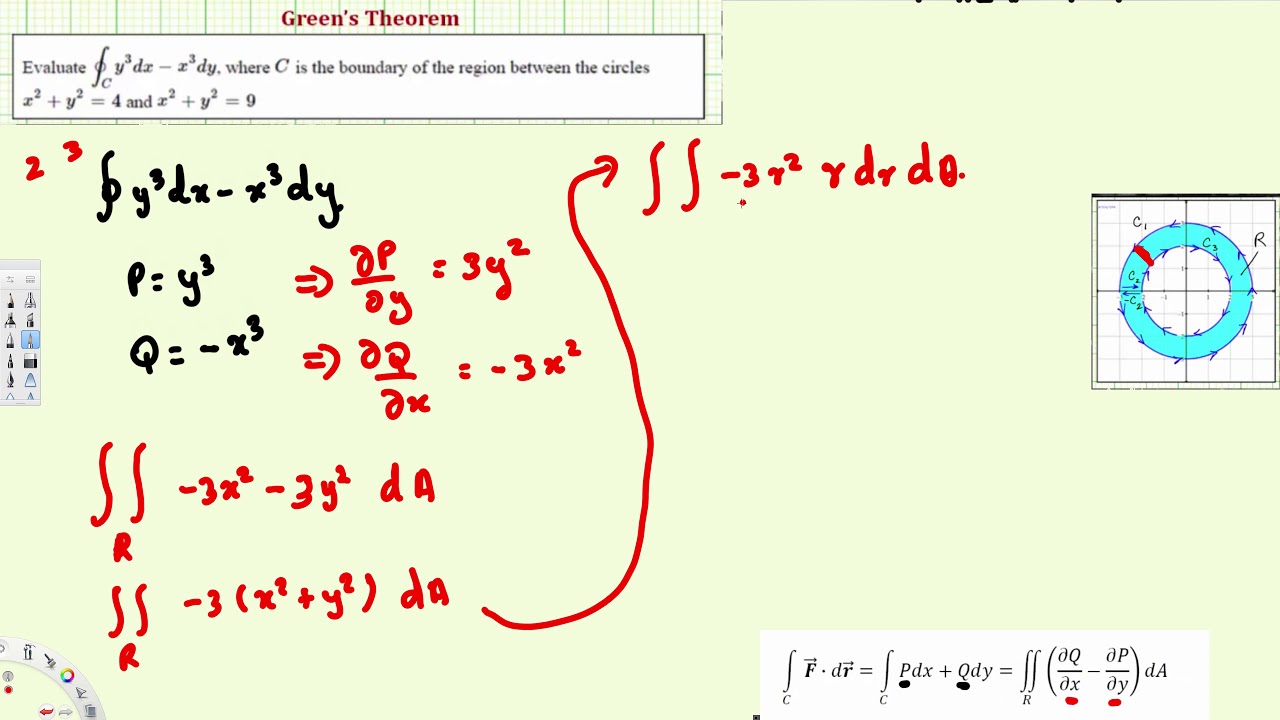
Greens Thm Parameterized Surfaces Math 240 Greens Theorem Calculating area Parameterized Surfaces Normal vectors Tangent planes Using Greens theorem to calculate area Example We can calculate the area of an ellipse using this method. Now using Greens theorem on the line integral gives C y 3 d x x 3 d y D 3 x 2 3 y 2 d A C y 3 d x x 3 d y D 3 x 2 3 y 2 d A. Consider the integral Z C y x2 y2 dx x x2 y2 dy Evaluate it when a Cis the circle x2 y2 1. A planimeter is a device used for measuring the area of a region. 1 Greens Theorem Greens theorem states that a line integral around the boundary of a plane region D can be computed as a double integral over DMore precisely if D is a nice region in the plane and C is the boundary of D with C oriented so that D is always on the left-hand side as one goes around C this is the positive orientation of C then Z.
Source: pinterest.com
Because of its resemblance. This is the currently selected item. Note that P y x2 y2Q x x2 y2 and so Pand Qare not di erentiable at 00 so not di erentiable everywhere inside the. Since D D is a disk it seems like the best way to do this integral is to use polar coordinates. In particular Greens Theorem is a theoretical planimeter.
Source: pinterest.com
Thanks to all of you who support me on Patreon. Do not think about the plane as. Now using Greens theorem on the line integral gives C y 3 d x x 3 d y D 3 x 2 3 y 2 d A C y 3 d x x 3 d y D 3 x 2 3 y 2 d A. Since D D is a disk it seems like the best way to do this integral is to use polar coordinates. Greens theorem is beautiful and all but here you can learn about how it is actually used.
Source: pinterest.com
In particular Greens Theorem is a theoretical planimeter. This is the currently selected item. We could compute the line integral directly see below. Consider P and Q to be the functions of x. Greens Theorem may seem rather abstract but as we will see it is a fantastic tool for computing the areas of arbitrary bounded regions.
Source: pinterest.com
The tangent vector. Lets see if we can use our knowledge of Greens theorem to solve some actual line integrals. The first form of Greens theorem that we examine is the circulation form. Greens theorem allows us to integrate regions that are formed by a combination of a line and a plane. In addition Gauss.
Source: pinterest.com
The tangent vector. Google Classroom Facebook Twitter. Greens theorem example 2. Let us solve an example based on Greens theorem. 3a Find the flux integral for the vector field F and the curve C.
Source: pinterest.com
1286 CHAPTER 18 THE THEOREMS OF GREEN STOKES AND GAUSS Gradient Fields Are Conservative The fundamental theorem of calculus asserts that R b a f0x dx fb fa. 3a Find the flux integral for the vector field F and the curve C. Greens Theorem Cauchys Theorem Cauchys Formula These notes supplement the discussion of real line integrals and Greens Theorem presented in 16 of our text and they discuss applications to Cauchys Theorem and Cauchys Formula 23. Greens theorem is beautiful and all but here you can learn about how it is actually used. But with simpler forms.
Source: pinterest.com
Greens theorem allows us to integrate regions that are formed by a combination of a line and a plane. Since D D is a disk it seems like the best way to do this integral is to use polar coordinates. Where D D is a disk of radius 2 centered at the origin. We could evaluate the line integral of Fdr along C directly but it is almost always easier to use Greens theorem. Ab R2 is a piecewise.
Source: pinterest.com
Our standing hypotheses are that γ. Greens theorem is beautiful and all but here you can learn about how it is actually used. Let C be a positively oriented smooth and closed curve in a plane and let D to be the region that is bounded by the region C. Particularly in a vector field in the plane. Consider the integral Z C y x2 y2 dx x x2 y2 dy Evaluate it when a Cis the circle x2 y2 1.
Source: pinterest.com
You da real mvps. A We did this in class. Circulation form of Greens theorem. You da real mvps. All of the examples that I.
Source: pinterest.com
D Q x P y d A C P d x Q d y provided the integration on the right is done counter-clockwise around C. We are taking C to have positive orientation. Particularly in a vector field in the plane. Now using Greens theorem on the line integral gives C y 3 d x x 3 d y D 3 x 2 3 y 2 d A C y 3 d x x 3 d y D 3 x 2 3 y 2 d A. But with simpler forms.
Source: pinterest.com
We could compute the line integral directly see below. This lecture discusses Greens theorem in the plane. Greens Theorem - Example 1 In mathematics Greens theorem also known as the divergence theorem or the fundamental theorem of calculus is a theorem in calculus in which the integral of a function over an arbitrary region in the plane is found by computing the line integral around any closed curve that intersects the region. Greens Theorem Example 2 Another example applying Greens Theorem Vector Calculus - What is Greens theorem. Greens Theorem JosephBreen Introduction OneofthemostimportanttheoremsinvectorcalculusisGreensTheorem.
Source: pinterest.com
Thanks to all of you who support me on Patreon. Greens theorem example 2. Greens theorem 1 Chapter 12 Greens theorem We are now going to begin at last to connect difierentiation and integration in multivariable calculus. A We did this in class. Because of its resemblance.
Source: pinterest.com
And actually before I show an example I want to make one clarification on Greens theorem. This is the currently selected item. We are taking C to have positive orientation. But we can compute this integral more easily using Greens theorem to convert the line integral into a double integral. Consider the integral Z C y x2 y2 dx x x2 y2 dy Evaluate it when a Cis the circle x2 y2 1.
Source: pinterest.com
And actually before I show an example I want to make one clarification on Greens theorem. That is we are traversing it in the counter-clockwise direction. Using Greens Theorem to solve a line integral of a vector fieldWatch the next lesson. Since D D is a disk it seems like the best way to do this integral is to use polar coordinates. But with simpler forms.
Source: pinterest.com
1286 CHAPTER 18 THE THEOREMS OF GREEN STOKES AND GAUSS Gradient Fields Are Conservative The fundamental theorem of calculus asserts that R b a f0x dx fb fa. 1 Greens Theorem Greens theorem states that a line integral around the boundary of a plane region D can be computed as a double integral over DMore precisely if D is a nice region in the plane and C is the boundary of D with C oriented so that D is always on the left-hand side as one goes around C this is the positive orientation of C then Z. Particularly in a vector field in the plane. You da real mvps. And actually before I show an example I want to make one clarification on Greens theorem.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title greens theorem example by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
