Your Inequality with no solution example images are ready in this website. Inequality with no solution example are a topic that is being searched for and liked by netizens today. You can Get the Inequality with no solution example files here. Download all free photos.
If you’re looking for inequality with no solution example images information connected with to the inequality with no solution example keyword, you have come to the ideal site. Our site frequently gives you hints for viewing the highest quality video and picture content, please kindly surf and find more informative video content and images that match your interests.
Inequality With No Solution Example. Solve the rational equation. The final solution is the intersection of the solutions of the independent inequalities if we have and between them. Example 2x 1 3 is an inequality. To be a solution of an or inequality a value has to make only one part of the inequality true.
Absolute Value Equations With No Solution Expii From expii.com
Example The solution to the inequality 2x 1 3 is the set of all x 1. 3 25 2 15 1 05 Ð 05 Ð 1 Ð 1. If you graph the 2 inequality solutions you can see that they have no values in common. The final solution is the intersection of the solutions of the independent inequalities if we have and between them. This means no matter what number you plug into x the inequality x 1 will never be true. There is no real number that we can substitute into eqx 5 x 7 eq in order to make a true statement.
3 m 4 3 m 9.
Example 2x 1 3 is an inequality. Example 3 has no solution. X 4 7. If the inequality states something untrue there is no solution. 5 is not greater than 7 and so this inequality has no real solution. Now divide each part by 2 a positive number so again the inequalities dont change.
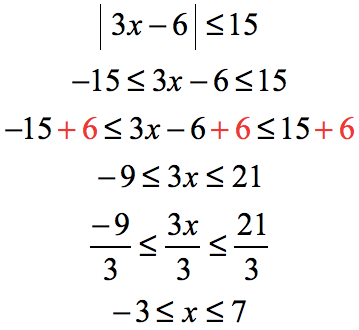Source: chilimath.com
And that is the solution. The solution to this compound inequality is all the values of x in which x is either greater than 6 or x is less than 2. Now divide each part by 2 a positive number so again the inequalities dont change. 10 t 45 2 5 t 23 The third example evaluates to. 5 is not greater than 7 and so this inequality has no real solution.
Source: expii.com
If there is a and between the independent inequalities the final solution is the intersection of their solutions. 6 x 3. For example x 6 or x 2. Check the solutions in the original equation to be sure they work. To solve inequalities in this example simply answer each inequality separately and then determine the final solution using the principles below.
Source: youtube.com
5 is not greater than 7 and so this inequality has no real solution. 10 t 45 2 5 t 23 The third example evaluates to. So the first and last regions will be part of the solution. An intersection of 2 sets is where the sets overlap or which values are in common. Maybe they have no solution because the coefficients of the variables are the same on both.
Source: courses.lumenlearning.com
This is why the compound inequality has no solution. Maybe they have no solution because the coefficients of the variables are the same on both. There is no real number that we can substitute into eqx 5 x 7 eq in order to make a true statement. Since this is a greater than inequality the solution can be rewritten according to the greater than rule. But to be neat it is better to have the smaller number on the left larger on the right.
Source: expii.com
And that is the solution. If you graph the 2 inequality solutions you can see that they have no values in common. For example x 6 or x 2. 3 25 2 15 1 05 Ð 05 Ð 1 Ð 1. 5 is not greater than 7 and so this inequality has no real solution.
Source: expii.com
There is no overlap in their 2 sets. Check the end point of the first related equation 7. There is no real number that we can substitute into eqx 5 x 7 eq in order to make a true statement. 3 m 4 3 m 9. An inequality can have no solution and there are several cases where this can happen including.
Source: onlinemathlearning.com
Example 3 has no solution. Now multiply each part by 1. There is no real number that we can substitute into eqx 5 x 7 eq in order to make a true statement. If there is a and between the independent inequalities the final solution is the intersection of their solutions. Here is the solution in both inequality and interval notation form.
Source: courses.lumenlearning.com
To find the restrictions create an equation by. The final solution is the intersection of the solutions of the independent inequalities if we have and between them. X 4 7. To be a solution of an and inequality it must make both parts true. For example x 6 or x 2.
Source: chilimath.com
6 x 3. And that is the solution. To be a solution of an and inequality it must make both parts true. Express the solution as an inequality graph and interval notation. X - 9 -12.
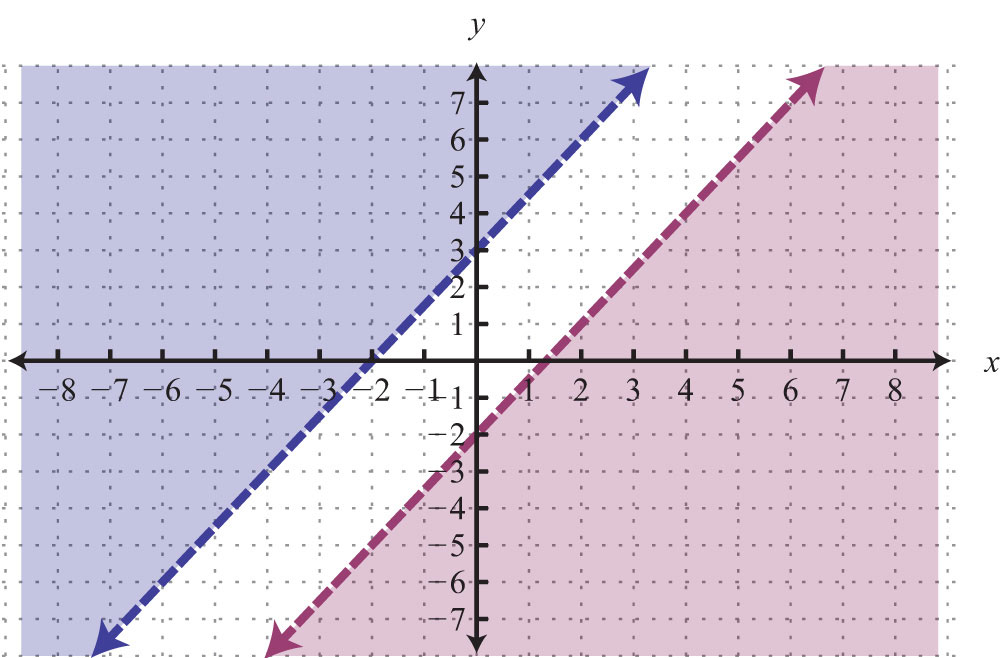Source: 2012books.lardbucket.org
Now divide each part by 2 a positive number so again the inequalities dont change. Solve the rational equation. Or indicates that as long as either statement is true the entire compound sentence is true. Now multiply each part by 1. Ive seen some equations and inequalities that have no solution.
Source: expii.com
The steps to solve linear inequalities are the same as linear equations except if you multiply or divide by a negative when solving for the variable you must reverse the inequality symbol. An intersection of 2 sets is where the sets overlap or which values are in common. Example 3 Solve x 1 for x. 5 is not greater than 7 and so this inequality has no real solution. Example The solution to the inequality 2x 1 3 is the set of all x 1.
Source: courses.lumenlearning.com
Here is the solution in both inequality and interval notation form. To be a solution of an or inequality a value has to make only one part of the inequality true. The final solution is the union of the solutions of the independent inequalities if we have or between them. This means no matter what number you plug into x the inequality x 1 will never be true. Examples of these are.
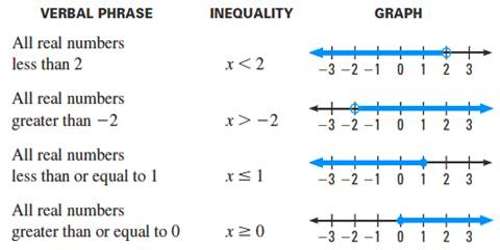Source: assignmentpoint.com
The steps to solve linear inequalities are the same as linear equations except if you multiply or divide by a negative when solving for the variable you must reverse the inequality symbol. 10 t 45 2 5 t 23 The third example evaluates to. Everything else on the graph is a solution to this compound inequality. Also in this case weve got an or equal to in the inequality and so well need to include the endpoints in our solution since at this points we get zero for the inequality and 0 ge 0 is a true inequality. 3 25 2 15 1 05 Ð 05 Ð 1 Ð 1.
Source: expii.com
If there is a and between the independent inequalities the final solution is the intersection of their solutions. Examples of these are. Because we are multiplying by a negative number the inequalities change direction. To be a solution of an and inequality it must make both parts true. Now multiply each part by 1.
Source: expii.com
Examples of these are. An inequality can have no solution and there are several cases where this can happen including. Just so why would an inequality have no solution. X - 9 -12. 3 25 2 15 1 05 Ð 05 Ð 1 Ð 1.
Source: youtube.com
X - 9 -12. There is no real number that we can substitute into eqx 5 x 7 eq in order to make a true statement. Examples of these are. If you graph the 2 inequality solutions you can see that they have no values in common. This set may have in nitely many numbers and may be represented by an interval or a number of intervals on the real line.
Source: pinterest.com
10 t 45 2 5 t 23 The third example evaluates to. The final solution is the intersection of the solutions of the independent inequalities if we have and between them. Ive seen some equations and inequalities that have no solution. The solution of an inequality is the set of all numbers which satisfy the inequality. Also in this case weve got an or equal to in the inequality and so well need to include the endpoints in our solution since at this points we get zero for the inequality and 0 ge 0 is a true inequality.
Source: khanacademy.org
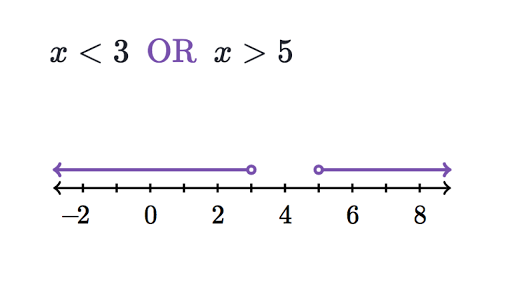
An inequality can have no solution and there are several cases where this can happen including. Check the end point of the first related equation 7. Now multiply each part by 1. Just so why would an inequality have no solution. This is why the compound inequality has no solution.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title inequality with no solution example by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
